Egy kis rémisztő matematika azoknak, akik szeretik. Vagy már régebben dolgoznak vektoros ábrákkal, de sosem értették, mi is van mögötte…

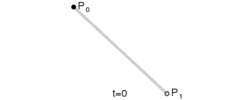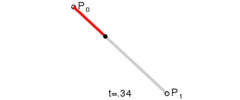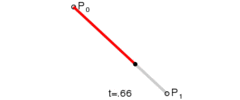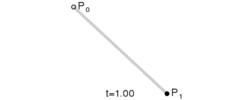
Az egyenes szakaszt elsőfokú Bézier görbével reprezentáljuk. A következő függvénnyel kiszámítva minden pont koordinátáját, egyszerűen végigmegyünk a két csomópont (P₀ ésP₁)közötti legrövidebb szakaszon¹.

B(t) = (1 – t) P₀ + t P₁ , ahol 0 ≤ t ≤ 1

1. ábra: Elsőfokú Bézier görbe (egyenes szakasz)

A másodfokú Bézier görbe egy parabolaív. Másodfokú függvényének képlete:

B(t) = (1 – t)² P₀ + 2(1 – t)t P₁ + t²P₂ , ahol 0 ≤ t ≤ 1

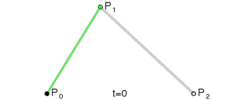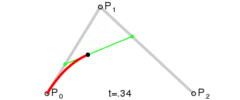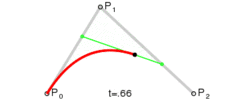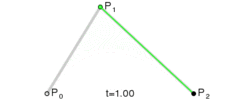
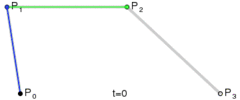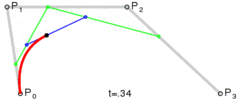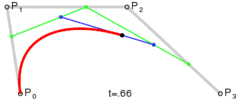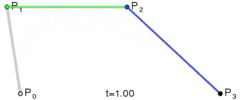
2. ábra: A másodfokú vagy kvadratikus Bézier görbe

Az első csomópont, az iránypont és a második csomópont egy háromszöget alkotnak. Az iránypont a görbe – útvonal – két csomópontjába húzott érintőinek metszéspontja.

A görbét a következőképpen képezhetjük: Indítsunk egyszerre egy kiskocsit az első csomópontból az iránypont felé, egy másik kiskocsit az iránypontból a második csomópont felé. A két kocsi között feszítsünk ki légvonalban egy rugalmas kötelet, ezen ugyanazon időben induljon el egy bogár az egyik kocsitól a másikig. Adott idő alatt mindhármójuknak célba kell érni. A két kocsi egyenes pályán halad. A bogár viszont egy parabolaív alakú pályát jár be a síkban, miközben ő úgy érzi, hogy mindig egyenesen halad a kötélen.

Ilyen kvadratikus, másodfokú Bézier görbéket használnak a True Type fontok, betűtípusok leírásához vagy az MS Paint program íveinek szerkesztéséhez.

A harmadfokú vagy köbös Bézier görbe a legáltalánosabb, minden vektorgrafikus program által használt megvalósítása a pontok közötti útvonalak leírásának. Klasszikus formája: két csomópont az útvonal végén, két iránypont mindegyik csomóponthoz kapcsolva, melyeket összekötve csomópontjukkal, megkapjuk a csomóponthoz húzott érintőt. Az iránypont távolsága csomóponttól itt a görbülettel arányos.

Az előbbi mechanikus hasonlatunkkal: A kezdő csomópontból indítunk autót az első iránypontba, az első iránypontból a második iránypontba, a második iránypontból pedig a záró csomópontba. Egyszerre három autót. Minden autónak ugyanannyi ideje van elérni a célját. Feszítsünk ki újra rugalmas köteleket az első-második és a második-harmadik autó közé. A korábbi módszerrel indítsunk el két bogarat a kifeszített kötélpályákon. Hogy a képzeletünket még inkább megterheljük, a két bogár között is feszítsünk ki egy kötelet, amelyen az egyik bogártól a másikig szaladjon át egy bodobács. A bogaraknak és a bodobácsnak is célba kell érni, míg az autók beérnek. A bodobács így az első csomópontból a másodikba jut, miközben egy görbe útvonalat ír le.

A bodobács által leírt pálya függvénye ebben az esetben:

B(t) = (1 – t)³ P₀ + 3(1 – t)²t P₁ + 3(1 – t)²t P₂+ t³P₃ , ahol 0 ≤ t ≤ 1

3. ábra: A harmadfokú vagy köbös Bézier görbe

A köbös Bézier görbéket ebben a formában használják a vektorgrafikus programokban. Az ábrát kicsit leegyszerűsítve megkapjuk az útvonalvégi két csomópontot és az iránypontokat, melyek meghatározzák a görbületet.

Ha tovább növeljük a Bézier görbék fokszámát, olyan görbéket kapunk, melyeknél a két végponthoz, csomóponthoz kettőnél több iránypont is tartozik. A végpontok között e módszerrel egészen bonyolult, kacskaringózó görbéket is le tudunk írni. A gyakorlatban ezek a összetettebb görbék mindig visszavezethetők több szegmensű, harmadfokú Bézier görbékre. Főleg térbeli modellező programoknál használják ezeket az n-edfokú görbéket, úgynevezett „spline”-okat, vagy NURBS² görbéket.